Babylonian 'algebra' from Crest of the Peacock

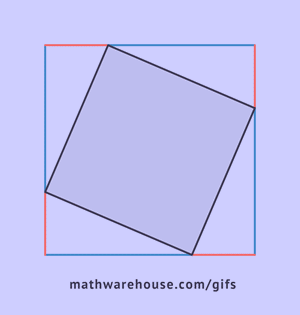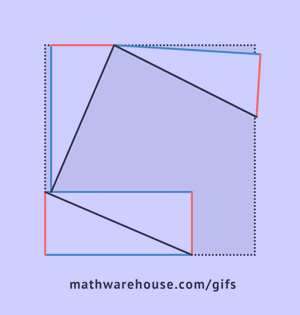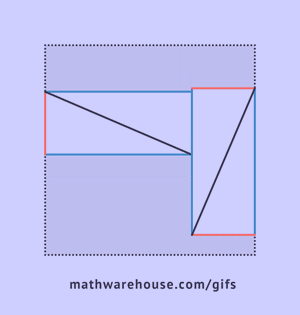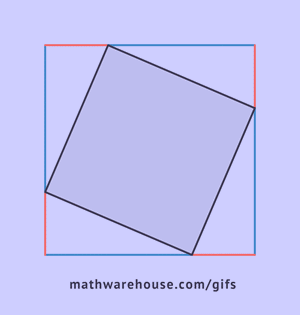
What first stood out to me after reading this section of Crest of the Peacock, was how expansive the world of mathematics can be, but also how much there is I haven't explored of it. Before reading this section, I read the question on the blog "how could one state a general mathematical principle in a time before the development of algebra and algebraic notation?", and at first I couldn't come up with anything. I think this is because I've never been taught of any other way than using algebraic notation, and teachers never asked me to come up with ways to do so! It seems that the Babylonians used a terminology instead of symbols though, using terms such as ush, sag, lagab, sukud, asha, and sahar to represent terms such as length, width, and square. Instead of saying XY = X*Y they would say Asha (area) = Ush (length) multiplied by Sag (breadth/width). In a way, using words instead of notation, turns the word into a notation of sorts --an odd paradox.

I believe that mathematics is all about generalizations and abstractions. I see generalizations in mathematics in the forms of rules, equations, and formulas. Generalizations often allow users to have a base-level (instrumental) understanding of how to do basic arithmetic and find relationships within each problem. However, abstractions give the individual a wider scope of the world, and the applications math can have in the real world. Abstractions in math reveal a deeper understanding and need to apply the generalities in a more focused sense. An example would be from one of the readings we had: giving an area question with differing units. The generalization would be knowing how formulas work, knowing that the area of a rectangular space is length x width, but the abstraction comes from the deeper understanding of conversion so the units are all uniform. This also has real world application!

The first that came to mind that mind that could be explained without algebra would be areas of mathematics that rely heavily on visualization. Pulling from the readings, geometry would be one that could be incorporated without algebra (although it would be difficult). The hindrance would come from not having algebraic notations, but the overall lessons could be taught visually, as a core concept of geometry is to use visualization. Another area could be basic algebra for younger students, like finding x or y, using basic arithmetic. A visual representation using blocks for example could relay the question "If 5 - x = 2, what is x?"; 5 interlocking blocks could be on one side and 2 on the other, and the student has to find the difference.

Babylonian-style Base 60 Multiplication table for 45

Col 1         Col 2

3     <-->     15

4     <-->     11, 15  --> EXPLANATION: 45/4 = 11.25 --> in base 60... 11.25 <--> 11 + (15/60)

5     <-->     9

6     <-->     7, 30  --> EXPLANATION: 45/6 = 7.5 --> in base 60... 7.5 <--> 7 + (30/60)

9     <-->     5

10   <-->     4, 30 --> EXPLANATION: 45/10 = 4.5 --> in base 60... 4.5 <--> 4 + (30/60)

12   <-->     3, 45 --> EXPLANATION: 45/12 = 3.75 --> in base 60... 3.75 <--> 3 + (45/60)

15   <-->     3

1, 12 <-->    37, 30 --> EXPLANATION: 45/(1+(12/60)) = 45/1.2 = 37.5 <--> 37 + (30/60)

1, 15 <-->    36 --> EXPLANATION: 45/(1+(15/60)) = 36 

1, 30 <-->    30   --> EXPLANATION: 45/(1+(30/60)) = 30

A response to The Crest of the Peacock

The ideas that shocked me throughout the chapter all revolve around colonialism and how it's affected our educational system and history. Throughout the entire chapter I kept saying to myself "I had no idea that happened...that's not what I remember learning", and all of this leads back to how our educational system is extremely Eurocentric and has somewhat altered the past to discredit, or not acknowledge, other great mathematicians.

One of the most interesting pieces of information was about the exchange of knowledge, and how much more was learned from the east than originally given credit for. Asians, Egyptians, Babylonians and Arabs are all some of the people mentioned and credited in this article who helped teach many famous Greek mathematicians and theorists; yet the only ones credited are the Greeks. For example, it mentions that even Pythagoras, famous for the Pythagorean theorem, traveled as far as India to explore and gain knowledge; yet throughout my entire grade school history I never heard of this. I wonder how my views would change had I learnt the importance the east had for influencing western European mathematics.

A second interesting point, that raised many questions, was about the Mayan civilization in Central America. They were able to create a place-value system, but also explore astronomy with limited tools and technology. I would be very interested to learn more about their systems and how they could accomplish such feats 

A final part that made me extremely interested was about the Bait al-Hikma (House of Wisdom), which served as almost a campus for intellects to exchange information, learn, and research...oh how it cool it must be to be a fly on the wall in there. To me, the most interesting part was how it brought in people from all over, not just individuals located in Baghdad. The idea of a group of multicultural individuals coming together to share knowledge to progress the art of mathematics was extremely interesting...I don't know why but when I think of older times, I think of less exploration, and more of individuals learning within their home countries. I believe this comes from that Eurocentric ideology where Greek mathematicians are solely credited, and not the others who may have taught them...it makes it seem as if they came up with their theories on their own and had no help.

Babylonian Mathematics and the Curious Case of Base 60

Mathematics has had a place in history for hundreds of thousands of years; notably, the Babylonians used a base 60 place value system, a stark contrast from the base 10 we use now. When first asked about why they may have used base 60, I immediately came to a halt. Why would they? What's the relevance? It wasn't until I read the next question, asking how we still use 60s in our daily lives that allowed me to spark a train of thought. The first notable 60 used to today is in the context of time: 60 seconds is 1 minute, and 60 minutes is 1 hour. Although notable, this doesn't answer why 60 was used. I believe 60 was used however because of how it's easily divisible. I remember learning in a number theory class that 60 is the only number that can be divided by 1,2,3,4 and 5; with this in mind, it is possible 60 was used because we can divide 60 into half, thirds, quarters, fifths, sixths, and tenths (of course we can divide 60 into twentieths, thirtieths and other factors, but we don't have that many fingers)! This would make 60 a really desirable number as time could work in ones favor without having a clock. The idea of not having a clock also feeds into my next area of notability: the circle. Now the circle is not 60 degrees in nature, but like the division argument made earlier, the circle is divisible by 60 degrees.

Perhaps Babylonians were able to find out that a circle was 360 degrees, and with their knowledge of ratios and 60s, theycould use such inventions as sun dials. This would allow the Babylonians to have a makeshift way of telling the (exact) time. 

From the site Thoughtco.com's Babylonian Mathematics and the base 60 System (linked below), it's interesting to see that the reason why Babylonians used base 60 was similar to my argument of having more factors. In the article, it mentions that base 60 has factors of 1,2,3,4,5,6,10,12,15,20,30 and 60 while base 10 only has 1,2,5, and 10; in fact it's actually pointed out by the Times that the number 60 "has more divisors than any smaller positive integer" which is something I didn't know before. What was also interesting was the way they invented the systems using their hands as well. As noted above, we use a base 10 because we can count 10 on our fingers, but it doesn't seem possible to count to 60 on our fingers alone. However, the Babylonians apparently used their hands as well, using one hand to count to twelve, and the other 5 fingers counting groups of 12 --> 5 x 12 =60! The way they counted the 12 was by using the index to pinkie fingers' joints (tip, middle joint, and where the finger meets the knuckle), 3 'joints' connected to 4 fingers is 12. This was mind blowing to me, and shows how 60 is still able to be divided and counted through fingers. 

ABC Science also wrote about how the Babylonians told time, saying that "...their division of a day into 360 parts called 'ush' that each equaled four of minutes in our time system". There is also hints that the Babylonians thought that there were 360 days in the year, which is not far off from the 365 day calendar we use now. If this is true, ancient Babylonians may have influenced modern day astrology into how we perceive our heliocentric model of the solar system. 

Another way that Babylonians influenced modern day mathematics is through their writing and documentations of numbers. The Babylonians had a symbol for 10 and a symbol for 1s, when they were grouped together you can easily read, for example (<< YYY) as the number 23 --> 2 groups of 10 and 3 1s. This is very similar to how we teach younger students now. When we show them the number 28, we tell them it's 2 10s and 8 1s, sometimes even using blocks to represent a 10 vs a 1 (refer to picture). 

https://www.thoughtco.com/why-we-still-use-babylonian-mathematics-116679#:~:text=Babylonian%20math%20has%20roots%20in,according%20to%20%E2%80%8BUSA%20Today.&text=When%20the%20two%20groups%20traded,multiplied%20by%2012%20equals%2060.

https://www.abc.net.au/science/articles/2011/11/15/3364432.htm#:~:text=Ancient%20Babylonians%3A%20hours%20and%20minutes,60%20plus%20two%20or%20182.

A response to Integrating history of mathematics in the classroom

 

    

I believe that math history should be incorporated into math teaching, but not in a surface-level way. When people usually hear the word ‘history’ they associate it with facts and historical figures; in the context of math, it doesn’t seem all too important to know where or when Pythagoras lived. And to that extent, I do agree, if math history is incorporated as just who the mathematician was and what he did, it doesn’t serve much purpose. However, where math history can insight more critical thinking is when the mathematicians’ downfalls and struggles can be used in the class. As the article states, we can use the failures of a historical math figure to pose different questions that may engage students more than just giving them a worksheet with questions. This would be a way to implement more relational learning into the course and reduce instrumental learning. Instead of memorizing rules to solve a particular question, students will be forced to engage with (real life) struggles and problems these famous mathematicians faced. It could open up new interests and avenues to the students learning and give a better understanding of the material too. When I first heard the term ‘math history’ I originally thought it would mindless facts that served no use to a students’ goals, but after reading the article my thoughts on it have changed.

One of the main ideas that had me stop during the readings was during the section of Historical Snippets, the sections in math textbooks having incorporated historical information. I remember during grade school, whenever I saw a historical snippet, I was always detracted by the subject material and often skipped it. To preface, I’m not much of a history person to begin with, but much like the article states, I believe I was also predisposed to not engage with the material as I didn’t see it as beneficial to my learning / goals in the course. I believe this predisposition came from how my teachers hardly acknowledged these sections while teaching the course, giving me the impression that it wasn’t important. Further, the Historical Snippets were very surface level information that didn’t pose or solve any problems that challenged the reader, instead it was mostly tangential, expository information that provided no further involvement. However, another idea that made me stop and wonder how I may be able to incorporate mathematical history into lesson with historical arguments / problem solving. The most interesting part of the article to me was how we can use history, mainly as a tool to pose interesting problems to students to make them engage with course material more than just doing practice questions. I believe that the historical argument approach allows students to flex their minds creatively and look for alternative solutions to historical problems, which may also give some students who struggle with the material another avenue to understand and interact with the course. A final section that made me stop in the reading was the idea of using math historians as examples of failure and perseverance. We’re often told about a mathematician who came up with a theory, and it seems like they were able to do it in an afternoon, but this isn’t the truth at all! I believe we can use history as a teaching tool that extends beyond the course material to teach students about perseverance in the face of failure. It’s very cliché, but “Rome wasn’t built in a day”, and using mathematicians can give real life examples of how learning is a process and life-long; hopefully these mathematicians can be role-models for future students.

Hello World

 Hi my name is Tyler and this is my EDCP 442 blog